黑洞,是爱因斯坦广义相对论的预言之一,也是部分大质量恒星的归宿。由于黑洞的质量和密度都远大于一般恒星,使得广义相对论效应在黑洞周围极其明显,黑洞也因此成为人们关注的热点。在宇宙中广泛存在的是含有自旋(自转)、不含电荷的科尔黑洞(Kerr Black Hole)和既含自旋也具有电荷的科尔-纽曼黑洞(Kerr-Newman Black Hole)。这类致密天体既是引力波的理想辐射源,也是探寻宇宙和星系起源、演化的关键媒介。研究黑洞周围的时空性质,有助于人们检验广义相对论,在引力理论的发展、完善方面也具有重要意义。人们无法直接观测黑洞周围的时空几何。
研究小组通过建立试验粒子在黑洞附近的运动方程,观察粒子的运动特征来间接分析黑洞周围的时空性质,试验粒子的运动方程为常微分方程,需要借助数值积分算法求解。在保守系统中,体系能量是重要守恒量,一定程度上决定了整个体系的动力学状态,在积分求解过程中,保持体系能量守恒尤为关键。他们将哈密顿正则方程离散化,构造了适用于此情况的严格保能量算法。此算法具有极高的能量精度,并能长时间稳定。利用此算法,模拟试验粒子在科尔-纽曼黑洞周围的运动轨迹,并分析了试验粒子的动力学特征,发现当黑洞自旋a较小(时空拖曳现象不明显)、试验粒子角动量L较小时,试验粒子容易产生强混沌运动。
论文以“6维哈密顿系统保能量算法的构造”(Construction of second-order six-dimensional Hamiltonian-conserving scheme)为题被国际天体物理重要杂志《The Astrophysical Journal Supplement Series》(简称ApJS, IF: 8.136)接收发表。
本文的研究属于天体力学、计算物理、非线性动力学、黑洞物理和广义相对论的交叉融合领域,内容丰富,填补了二阶保能量算法在6维哈密顿系统中应用的空白;文中的动力学分析也为寻找试验粒子在黑洞周围的混沌区域提供了指导。
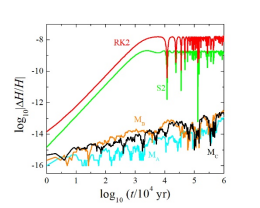
图一 左:不同算法的能量误差图,MC为本文构造的6维保能量算法,该算法可以在100亿年内将体系能量误差控制在10-13以下,为得到精确的数值解提供保障;
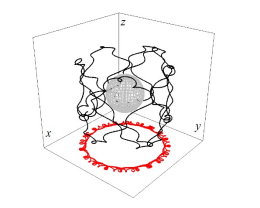
右:试验粒子在科尔-纽曼黑洞周围的轨迹示意图(黑色),红色为轨迹在xoy面的投影,灰色为黑洞的视界面。

图二 试验粒子在科尔-纽曼黑洞周围的动力学性质。
蓝色表示带电粒子在该区域为有序运动;左下角(红色及粉色区域)表示粒子处于强混沌状态。
论文作者:胡诗杨(博士生),伍歆教授(通讯作者),梁恩维。

 联系地址:广西区南宁市大学东路100号
联系地址:广西区南宁市大学东路100号 联系电话:0771-3237386
联系电话:0771-3237386 邮 编 :530004
邮 编 :530004